[자료구조] 그래프(Graph)

그래프(Graph)란?

그래프는 여러 개의 점(노드, 정점)과 그 점들을 연결하는 선(간선)으로 이루어진 자료구조

예를 들어:

• 지하철 노선도 → 역 = 노드, 역과 역을 연결하는 선 = 간선
• SNS 친구 관계 → 사람 = 노드, 친구 관계 = 간선
• 웹페이지 링크 구조 → 페이지 = 노드, 링크 = 간선

즉, 어떤 것들 사이의 연결 관계를 표현하기 좋은 자료구조가 그래프

 

그래프와 관련된 용어

• 정점(Vertex) : 노드(node) 라고도 하며 정점에는 데이터가 저장된다. (0, 1, 2, 3)
• 간선(Edge) : 정점(노드)를 연결하는 선으로 link, branch 라고도 부른다.
• 인접 정점(adjacent Vertex) : 간선에 의해 직접 연결된 정점 (0과 2은 인접정점)
• 단순 경로(simple path) : 경로 중에서 반복되는 정점이 없는 경우. 한붓그리기와 같이 같은 간선을 지나가지 않는 경로 ( 0->3->2->1 은 단순경로 )
• 차수(degree) : 무방향 그래프에서 하나의 정점에 인접한 정점의 수 (0의 차수는 3)
• 진출 차수(in-degree) : 방향 그래프에서 외부로 향하는 간선의 수
• 진입 차수(out-degree) : 방향 그래프에서 외부에서 들어오는 간선의 수
• 경로 길이(path length) : 경로를 구성하는데 사용된 간선의 수
• 사이클(cycle) : 단순 경로의 시작 정점과 종료 정점이 동일한 경우

---

그래프의 종류

🔹 1. 무방향 그래프 (Undirected Graph)

A — B
처럼 양쪽으로 연결된 상태.

A에서 B로 갈 수 있고, B에서 A로도 갈 수 있음.

예: 친구 관계, 양방향 도로 등

---

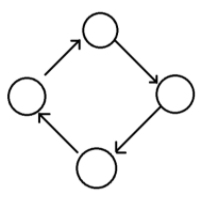
🔹 2. 방향 그래프 (Directed Graph, Digraph)

A → B
처럼 한쪽 방향으로만 연결된 그래프.

예:

• 인스타그램 팔로우 (내가 팔로우해도 상대가 안할 수 있음 → 단방향)
• 웹페이지 링크 구조

---

🔹 3. 가중치 그래프 (Weighted Graph)

간선에 비용 or 거리 같은 값이 붙어 있는 그래프.

예:

A —(5)— B
B —(2)— C

이때 5, 2 같은 숫자를 가중치(weight)라고 한다.

🚗 예: 네이버 지도 경로 찾기 —> 도로 거리(가중치)를 고려하여 최단 거리 탐색.

 

---

그래프를 코드로 표현하는 방법

1. 인접 리스트 (Adjacency List)

각 노드가 ‘연결된 노드 목록’을 갖는 방식.

// A: [B, C]
// B: [A, D]
// C: [A]
// D: [B]
const graph = {
  A: ["B", "C"],
  B: ["A", "D"],
  C: ["A"],
  D: ["B"]
};

 

✔ 장점: 메모리 적게 사용
✔ 단점: 두 노드가 연결됐는지 확인하려면 리스트 탐색해야 함

 

2. 인접 행렬 (Adjacency Matrix)

노드 개수만큼의 N×N 2차원 배열로 연결 여부를 표시.

예시(1: 연결, 0: 없음):

	A	B	C
A	0	1	1
B	1	0	0
C	1	0	0

const graph = [
  [0, 1, 1],
  [1, 0, 0],
  [1, 0, 0],
];

 

✔ 장점: 연결 여부를 O(1)에 바로 확인
✔ 단점: 메모리 많이 사용

 

---

그래프에서 자주 쓰는 알고리즘

1) BFS (너비 우선 탐색)

가까운 노드부터 넓게 탐색
➡ 미로 최단거리, 지하철 최소 환승 등에서 사용

2) DFS (깊이 우선 탐색)

한 방향으로 깊게 탐색
➡ 경로 찾기, 사이클 탐지 등에 사용

 

2025.11.04 - [개발지식/자료구조] - [자료구조] 탐색(검색) 알고리즘 (Search Algorithm)

[자료구조] 탐색(검색) 알고리즘 (Search Algorithm)

3) 최단 경로 알고리즘

가중치 그래프에서 특정 노드까지 최단 거리 찾기

• 다익스트라
• 벨만–포드
• 플로이드–워셜

---

 

그래프 vs 트리 차이 정리

구분	그래프(Graph)	트리(Tree)
구조	자유로운 연결 구조	계층(부모-자식) 구조
방향	방향/무방향 모두 가능	대부분 방향 그래프 형태(부모 → 자식)
사이클	있을 수도 있음	❌ 절대 없음 (Cycle 금지)
루트(시작점)	없음	있음 (Root 1개)
부모-자식 개념	없음	있음
두 노드 간 경로	여러 개일 수 있음	항상 1개만 존재
예시	지하철 노선도, SNS 관계, 최단 거리 알고리즘 ➡ 구조가 단순 히 위아래가 아니라 “네트워크”일 때	폴더 구조, DOM 구조 ➡ 계층 관계가 명확할 때

트리는 “사이클 없는 그래프”이고, “부모–자식 구조”가 명확한 특별한 그래프이다.

그래프 = 모든 연결 구조
트리 = 그중 “계층 구조”를 가진 특수한 그래프

트리도 결국 “노드 + 간선”으로 구성돼 있으니까 그래프의 한 종류이다.
하지만 아래 조건이 추가된다.

✔ 트리는 반드시 사이클이 없다 (A → B → C → A X)
순환되면 트리가 아님!

✔ 트리는 반드시 루트(root)가 1개
루트 기준으로 아래로 뻗어나가는 구조.

✔ 트리는 두 노드 사이의 길이 항상 딱 1개
그래프에서는 A → B로 가는 길이 여러 개일 수 있다.

 

---

그림으로 비교(개념)

✔ 그래프(사이클 가능)

A --- B
|    /
|   /
C --

 

✔ 트리(사이클 없음)

   A
  / \
 B   C
    / \
   D   E

---

참고 : https://hongcoding.tistory.com/78